How to Draw Opposing Fibonacci Spirals
As you already know I have been exploring geometric drawing with the ultimate goal of using these images in finished paintings. l plan on combining the geometry with my figures and/or launching into purely abstract works. A couple of weeks ago I decided to try opposing Fibonacci spirals. You've seen them in the heads of flowers, pine cones, pineapples and the really cool romanesco vegetable. I didn't think it would be too hard. I'd focus, accept some trial and error, focus some more and I'd get it. It turned out to be a fairly harrowing experience, with mind bending twists and turns (pun intended), frustrations that caused marital problems, grouchiness, and general malaise until I figured it all out. See the dramatic pictoral journey recreated here.
Fibbonacci Sprial How Not to do it. This is my first try. I want to see if I can find a way to do it without looking it up on the web or in a book. Clearly this is not the way to go.
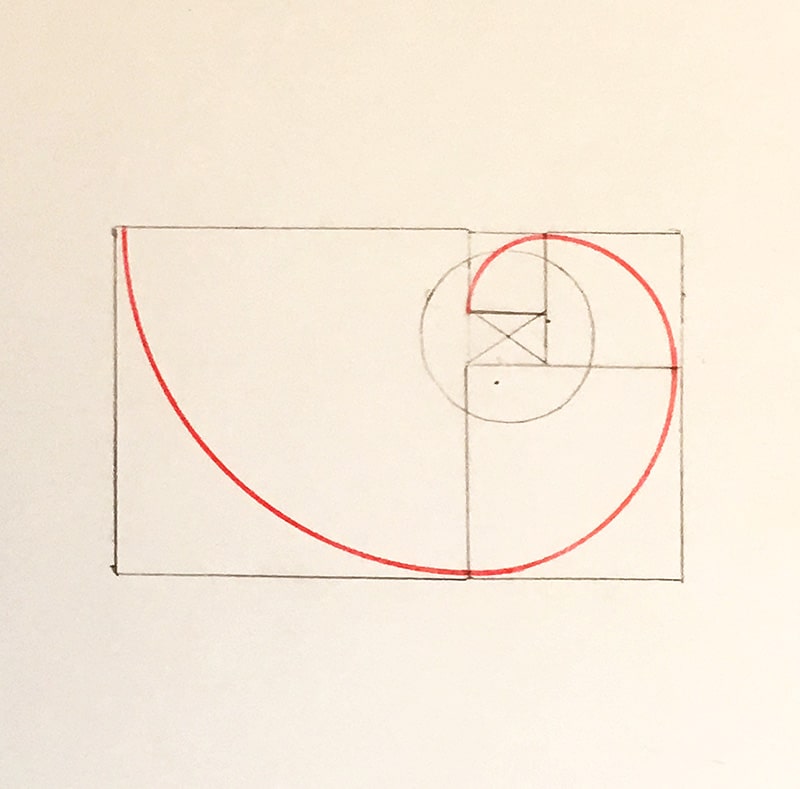
So I look it up online and find many videos showing how to draw single Fibonacci spirals using squares to find the point for the compass and draw an arc. Ok so fine, but how do you draw multiple-armed spirals and where do you start each arm? Clearly this attempt is not right. The arms should not cross.
I know! The spirals have to originate from the same point in the very center. So I try it but the arms obviously are going to cross if I keep going.
I can figure this out. Using precut paper templates to trace my squares and help me figure out where to start the spirals I dive into a five armed spiral.
Sure enough. There it is. The arms crash into their neighbor. I become grouchy and irritated and walk around the house scowling. This is what is often referred to as the artistic temperament.
Well, it's an OK drawing, but it's not what I want. So I go in the house and ask Giuliana, "Where do I start the spirals?" Together we look more closely at images of spirals in books.
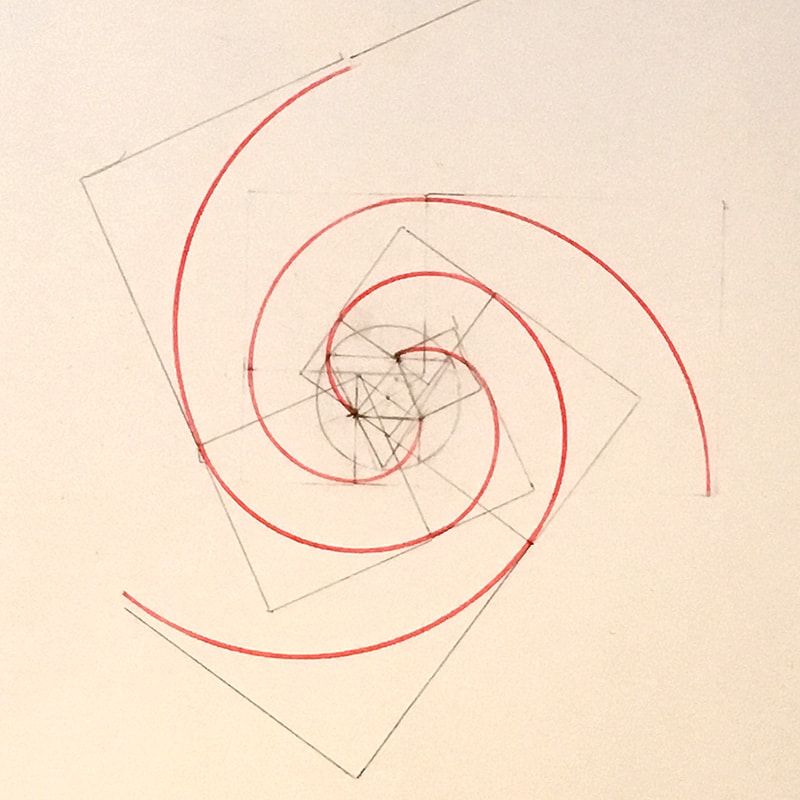
I start a three armed spiral. The center of the golden rectangle lines up with the center the triangle and the circle. The first square is spaced away from the center by half the width of the rectangle.
Here it is: My first 3-5 opposing Fibonacci spiral. You can see the horribly abused paper, but I did it! Hooray.
The Fibonacci sequence (1, 1, 2, 3, 5, 8, 13...) dictates the size of the squares that are used to draw the arcs. These drawings are actually a close approximation of the patterns we see in nature as an exact replication is not possible. What is interesting to note is that the websites and video tutorials that I found showed the spiral starting with two small squares. When I did multiple spirals this way the arms crossed. I ended up skipping one, so I did the # 1 square once, not twice, and spaced it out a bit from the center. I believe the actual way to do it would be to split the golden rectangle into a square and draw an arc, and keep doing that ad infinitum. Recommended books: Ruler and Compass by Andrew Sutton, Sacred Geometry by Stephen Skinner.